- and d. The estimated equation is:
_ _ Xi Yi Xi - Xn (Xi - Xn)2 ki --------------------------------------------------- 0 -2 -2 4 -2/10 = -.200 1 -1 -1 1 -1/10 = -.100 2 1 0 0 0 = .000 3 1 1 1 1/10 = .100 4 1 2 4 2/10 = .200 --------------------------------------------------- 10 0 0 10 0/10 = .000From the Table:
åi=1,5 ki = 0
åi=1,5 kixi = (-2/10)*0+(-1/10)*1+(0)*2+(1/10)*3+(2/10)*4 = 1
_
åi=1,5 ki2 = 1/[åi=1,5 (xi - Xn)2] = 1/10 =
= (-2/10)2 + (-1/10)2 + (0)2 + (1/10)2 + (2/10)2 =
= 10/100 = 1/10 = .100
^
b1 = åi=1,5 kiyi
= (-2/10)*-2 + (-1/10)*-1 + (0)*1 + (1/10)*1 + (2/10)*1
= (4+1+0+1+2)/10 = .800
^ _ ^ _
b0 = y - b1X = 0 - (8/10)*2 = -16/10 = -1.6
^
yi = -1.6 + .800*xi + ei
Which produces the fitted values:
^
yi = -1.6 + .800*xi
and the estimated residuals
^ ^
ei = ei = yi - yi = yi + 1.6 - .800*xi
This produces the table
^ ^ _
xi yi yi ei = yi - yi eixi yi - y
----------------------------------------------------
0 -2 -1.6 -.400 0.0 -2
1 -1 - .8 -.200 -.2 -1
2 1 0.0 1.000 2.0 1
3 1 .8 .200 .6 1
4 1 1.6 -.600 -2.4 1
----------------------------------------------------
10 0 0.0 0.000 0.0 0
-
SSE = åi=1,5 ei2 = -.42 + -.22 + 12 + .22 + -.62 = 1.6
_
SSTO = åi=1,5 (yi - y)2 = -22 + -12 + 12 + 12 + 12 = 8
SSTO - SSE 8 - 1.6
R2 = ---------- = --------- = .8
SSTO 8
s2 =
[åi=1,5 ei2]/(n - 2) = 1.6/(5-2) = .53333
^ _
s2{b1} = s2/[åi=1,5 (xi - X)2] = .53333/10 = .053333
^ _
s2{b0} = [s2åi=1,5 xi2]/{n[åi=1,5 (xi - X)2]}
= (.53333*30)/(5*10) = .31999
Hence:
^
s{b1} = .23094
^
s{b0} = .56568
The hypothesis test is:Ho: b1 = 0
H1: b1 ¹ 0
Our test statistic has a t distribution with n - 2 = 3 degrees of freedom:
^ ^
test statistic = (b1 - b1)/s{b1} = .800/.23094 = 3.4641
Using EVIEWS, P-Value (two-tail) = .04052.Ho: b0 = 0
H1: b0 ¹ 0
Our test statistic has a t distribution with n - 2 = 3 degrees of freedom:
^ ^
test statistic = (b0 - b0)/s{b0} = -1.6/.56568 = -2.8284
Using EVIEWS, P-Value (two-tail) = .06628.Below is the EVIEWS output. The first three columns of the table contain exactly the same values as those calculated in parts b, f and g respectively. As for the statistics below the table, we found R (R-squared) in part e, s (SE of regression) and the SSE (sum of squared residuals) in part f. The Mean of the dependent variable (Y) can be found in parts b,c or d. The 2 tail significance values below are the same as the ones computed above.
============================================================
LS // Dependent Variable is Y
Date: 03/02/98 Time: 22:21
Sample: 1 5
Included observations: 5
============================================================
Variable CoefficienStd. Errort-Statistic Prob.
============================================================
C -1.600000 0.565685 -2.828427 0.0663
X 0.800000 0.230940 3.464102 0.0405
============================================================
R-squared 0.800000 Mean dependent var 0.000000
Adjusted R-squared 0.733333 S.D. dependent var 1.414214
S.E. of regression 0.730297 Akaike info criter-0.339434
Sum squared resid 1.600000 Schwarz criterion -0.495659
Log likelihood -4.246107 F-statistic 12.00000
Durbin-Watson stat 1.725000 Prob(F-statistic) 0.040519
============================================================
The results of the simple linear regression are given below:
============================================================
LS // Dependent Variable is FUEL
Date: 03/02/98 Time: 22:29
Sample: 1 8
Included observations: 8
============================================================
Variable CoefficienStd. Errort-Statistic Prob.
============================================================
C 15.83786 0.801773 19.75353 0.0000
TEMP -0.127922 0.017457 -7.327679 0.0003
============================================================
R-squared 0.899489 Mean dependent var 10.21250
Adjusted R-squared 0.882737 S.D. dependent var 1.910451
S.E. of regression 0.654209 Akaike info criter-0.636340
Sum squared resid 2.567934 Schwarz criterion -0.616480
Log likelihood -6.806148 F-statistic 53.69488
Durbin-Watson stat 3.017045 Prob(F-statistic) 0.000330
============================================================
The plot looks like this: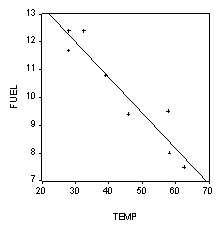
To find a point estimate of the expected value of fuel consumed when the average hourly temperature is 41, we simply plug 41 into our estimated equation:
^ ^ ^
yp = b0 + b1 xp = 15.83786 - .127922*41 = 10.593058
The 95% confidence interval for the point estimate in (c) is given by:
^ ^ _ ^
b0 + b1 xp ± t.025,n-2[s2(1 + 1/n) + (xp - X)2s2{b1}]1/2
Thus we find15.83786 - .127922*41 ± 2.447*[.6542092(1 + 1/8) + (41 - 43.975)2(.017457)2]1/2
and the confidence limits are: (8.8904, 12.2958)
============================================================
Dependent Variable: DCOUT
Method: Least Squares
Date: 03/03/98 Time: 14:56
Sample: 1 25
Included observations: 25
============================================================
Variable CoefficientStd. Errort-Statistic Prob.
============================================================
C 0.130875 0.125989 1.038779 0.3097
WIND 0.241149 0.019049 12.65927 0.0000
============================================================
R-squared 0.874493 Mean dependent var 1.609600
Adjusted R-squared 0.869036 S.D. dependent var 0.652278
S.E. of regression 0.236052 Akaike info criter 0.027090
Sum squared resid 1.281573 Schwarz criterion 0.124600
Log likelihood 1.661381 F-statistic 160.2571
Durbin-Watson stat 0.536610 Prob(F-statistic) 0.000000
============================================================
And here is a graph of the fitted function and the residuals: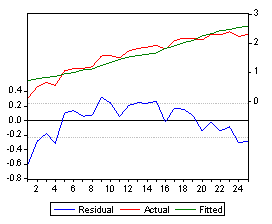
Below is the EVIEWS output for the paper strength example:
============================================================
Dependent Variable: TENSILE
Method: Least Squares
Date: 03/03/98 Time: 15:17
Sample: 1 19
Included observations: 19
============================================================
Variable CoefficientStd. Errort-Statistic Prob.
============================================================
C 21.32126 5.430178 3.926439 0.0011
HARDWOOD 1.770986 0.647814 2.733788 0.0141
============================================================
R-squared 0.305374 Mean dependent var 34.18421
Adjusted R-squared 0.264513 S.D. dependent var 13.77777
S.E. of regression 11.81589 Akaike info criter 7.876068
Sum squared resid 2373.458 Schwarz criterion 7.975482
Log likelihood -72.82264 F-statistic 7.473597
Durbin-Watson stat 0.246890 Prob(F-statistic) 0.014140
============================================================
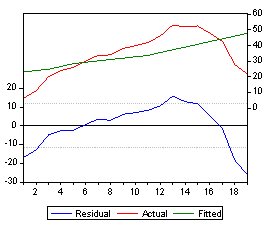
And here is a graph of the fitted function and the residuals: