45-733 PROBABILITY AND STATISTICS I Notes #5D


February 2000


Normal Distribution

  1. The Normal or Gaussian Distribution is written as:

    f(x) = {1/[(2p)1/2 s]} e-(x - m)2/ 2s2)              -¥ < x < +¥

    Where E(X) = m    and VAR(X) = s2

    The notation: X ~ N(m, s2) means that X is distributed as a Normal distribution with mean m and variance s2.

  2. The Standard Normal Distribution has a mean of zero and variance of one; namely,
          E(X) = m = 0, VAR(X) = s2 = 1.
  3. The distribution function of the Normal has its own symbol; namely:
           F(x) = F(x) = P(X £ x)
  4. The Normal is a unimodal, symmetric distribution so that the median, mean, and mode are all the same point. This symmetry makes it easy to calculate probabilities from any standard normal distribution function table. In particular, note that:
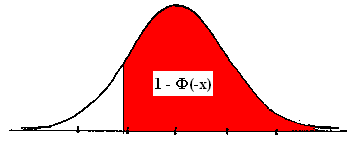
           F(x) = 1 - F(-x)    and     F(-x) = 1 - F(x)

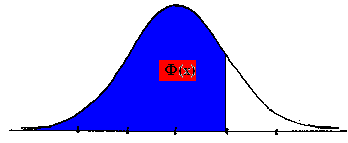
  5. Examples (assume X ~ N(0, 1))
    1. P(X £ 2) = F(2) = 1 - F(-2) = 1 - .0228 = .9772

    2. P(X £ -1) = F(-1) = 1 - F(1) = .1587.

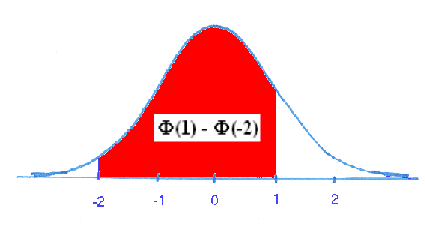
    3. P(-2 £ X £ 1) = F(1) - F(-2) = [1 - F(-1)] - F(-2) = 1 - .1587 - .0228 = .8185.

  6. Any Normal Distribution can be transformed into a Standard Normal Distribution through the linear transformation:
           Z = (X - m)/ s
    To see this, note that:
           E(Z) = (1/s)E(X) - (m/s) = 0
           VAR(Z) = VAR[(1/s)X - m/s)] = (1/s)2VAR(X) = 1
          Hence, Z ~ N(0, 1)
  7. Examples using X ~ N(3, 9)
    1. P(X £ 1) = P[(X - 3)/3 =< (1 - 3)/3] = P(Z £ -2/3) = F(-2/3) = 1 - F(2/3) = .2514
    2. P(-1 £ X £ 1) = P[(-1 - 3)/3 £ (X - 3)/3 £ (1 - 3)/3] = P(-4/3 £ Z £ -2/3) =
                      [1 - F(2/3)] - [1 - F(4/3)]       = .2514 - .0918 = .1596
    3. P(2X + 4 ³ 3) = P(2X ³ -1) = P(X ³ -1/2) = P[(X - 3)/3 ³ (-1/2 - 3)/3] =
                      P(Z ³ -7/6) = 1 - F(-7/6)       = 1 - .1210 = .8790
  8. Problem 4.43 p.156
    Let X = "resistance in ohms". We are given: m = .13 and s = .005.
    1. P(.12 £ X £ .14) = P[(.12 - .13)/.005 £ (X - .13)/.005 £ (.14 - .13)/.005] =
                      P(-2 £ Z £ 2) = F(2) - F(-2) = [1 - F(-2)] - F(-2)       = (1 - .0228) - .0228 = .9544
    2. (.9544)4
  9. Problem 4.45 p.157
    Let X = "width of a bolt". We are given: m = 950 and s = 10.
    1. P(947 £ X £ 958) = P[(947 - 950)/10 £ (X - 950)/10 £ (958 - 950)/10] =
                      P(-.3 £ Z £ .8) = F(.8) - F(-.3) = [1 - F(-.8)] - F(-.3)       =
                      (1 - .2119) - .3821 = .4060
    2. P(X < C) = .8531 = P[(X - 950)/10 < (C - 950)/10] = P[Z < (C - 950)/10]
      From the Distribution Function table for the Normal we see that above the point 1.05 is .1469 of the probability and below 1.05 is .8531 of the probability.
      Hence: (C - 950)/10 = 1.05 and C = 960.5
  10. Problem 4.46 p.157
    Let X = "score on Exam" and X ~ N(78, 36)
    1. P(X > 72) = P[(X - 78)/6 > (72 - 78)/6] = P(Z ³ -1) = 1 - F(-1) = 1 - .1587 = .8413
    2. P(X > C) = .1 = P[(X - 78)/6 > (C - 78)/6] = P[Z > (C - 78)/6] =
      1 - F[(C - 78)/6]
                      From the table 1 - F(1.28) = .1
                      Hence: (C - 78)/6 = 1.28 and C = 85.68
    3. P(X > C) = .281 = P[(X - 78)/6 > (C - 78)/6] = P[Z > (C - 78)/6] =
      1 - F[(C - 78)/6]
                      From the table 1 - F(.58) = .281
                      Hence: (C - 78)/6 = .58 and C = 81.48
    4. P(X < L) = .25 = P[(X - 78)/6 < (L - 78)/6] = P[Z < (L - 78)/6] = 1 - F[(L - 78)/6]
                      From the table 1 - F(.67) = F(-.67) = .25
                      Hence: (L - 78)/6 = -.67 and L = 74
                      Therefore: P(X > L + 5) = P[(X - 78)/6 > (79 - 78)/6] =
                            P(Z > 1/6) = 1 - F(1/6)       = .4325
    5. P(X > 84|X > 72) = P(X > 84 Ç X > 72)/P(X > 72) = P(X > 84)/P(X > 72)
                      P(X > 84) = P[(X - 78)/6 > (84 - 78)/6] = P(Z > 1) = 1 - F(1) = .1587
                      P(X > 72) = P[(X - 78)/6 > (72 - 78)/6] = P(Z > -1) = 1 - F(-1) = 1 - .1587 = .8413
                      Hence, P(X > 84|X > 72) = .1587/.8413 = .1886
  11. Random Sample
    Definition: A Random Sample is a set of independent and identically distributed random variables.
  12. Sample Mean
    _
    Xn = [åi=1,n Xi]/n
  13.     _
    E(Xn) = E{[1/n][X1 + X2 + ... + Xn]} = [1/n][E(X1) + E(X2) + ... + E(Xn)] =
                    [1/n][m + m + m + ... + m] = m
  14.           _
    VAR(Xn) = VAR{[1/n][X1 + X2 + ... + Xn]} =
                    [1/n]2[VAR(X1) + VAR(X2) + ... + VAR(Xn)] =
                    [1/n]2 [s2 + s2 + s2 + ... + s2] = (1/n)s2
  15. For all Distributions, the distribution of the sample mean has a mean equal to the true mean and a variance equal to the true variance divided by the sample size.
  16. If X1, X2, ... , Xn are independent random variables and Xi ~ N[mi, (si)2], then
    a1X1 + a2X2 + ... + anXn + b ~ N[(åi=1,n ai mi) + b , åi=1,n (ai)2 (si)2]
  17. Example: Let X ~ N(3, 9) and Y ~ N(5, 1)
    X + Y ~ N(8, 10)
    X - Y ~ N(-2, 10)
    2X - 3Y + 5 ~ N(-4, 45)
  18. Example: Suppose we have two populations, A and B, and we know that the distribution of scores in these two populations on an identical examination are normally distributed with the following parameters:
        X ~ N(625, 100) in population A
        Y ~ N(600, 150) in population B
        Suppose we take a random sample of two people from population A and a random sample of three people from population B. What is the probability that the average score of the two people from population A will be higher than the average score of the three people from population B. That is: 
           _    _      _    _
     P(X2 > Y3) = P(X2 - Y3 > 0)
             _
     Clearly X2 ~ N(625, 50)
             _
         and Y3 ~ N(600, 50)
        _    _
so that X2 - Y3 ~ N(25, 100)
          _    _
Hence: P[(X2 - Y3 - 25)/10 > (0 - 25)/10] = P(Z > -2.5) = 
            1 - F(-2.5) = 1 - .0062 = .9938