45-733 PROBABILITY AND STATISTICS I
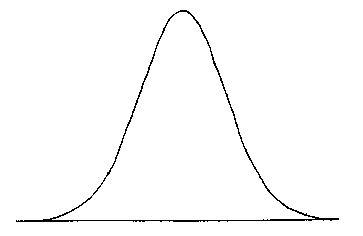
The Normal or Gaussian Distribution
The Normal or Gaussian Distribution is written as:
f(x) = {1/[(2p)1/2
s]}
e-(x - m)2/
2s2)
-¥ < x < +¥
Where E(X) = m and
VAR(X) = s2
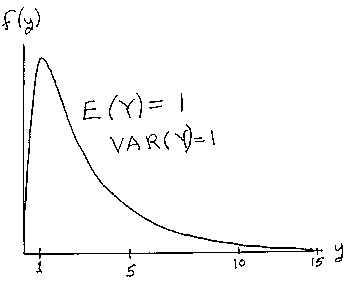
The log-normal distribution is the distribution of a random
variable whose natural logarithm follows a normal distribution. This
distribution is used in the Natural Sciences to model inherently postive
phenomenon such as size -- for example, by volume or weight. The growth of
bacteria colonies and of individual animals can be usefully analyzed using
the log-normal distribution.
If X ~ N(m, s2), then
Y = eX ~ log-normal. Namely:
f(y) = {1/[(2p)1/2
ys]}
e-(lny - m)2/
2s2)
Note that m and
s2 are the mean and
variance of X. The mean of Y is:
E(Y) = e[m + s2/2]
The Normal Distribution was discovered by Carl Friedrich Gauss (1777-1855).
Gauss was probably the greatest genius of whom there is any historical
record. Gauss could do arithmetic at the age of 3 and fortunately for the
history of humanity Gauss's unusual abilities drew the attention of the
Duke of Brunswick (northern Germany) who financed Gauss's education.
At the age of 14 or 15 Gauss discovered the
Prime Number Theorem
later proved by Riemann in 1896 (the Prime Number Theorem is concerned
with the average distribution of the Prime Numbers). About this time
Gauss also invented The Principle of Least Squares
which is the basis for all modern estimation methods. Just
this creation alone was a towering intellectual achievement of the first
order given its pervasive use throughout the Sciences.
Also about this time Gauss discovered (or created!) the
Normal Distribution in the theory of
probability.
At the age of 18 Gauss proved a beautiful theorem about
the constructability
of regular polygons by a ruler and compass -- a problem that had been worked
on since the Ancient Greeks. Gauss not only discovered a new constructable
Polygon -- 17 sided, the first in 2000 years -- he also proved a general
theorem about just what Polygons were constructable!
At the age of 21 in 1798, Gauss proved
The Fundamental Theorem of Arithmetic (every
integer greater than 1 can be expressed as a product of prime numbers).
One year later in 1799, Gauss proved
The Fundamental Theorem of Algebra (every
polynomial equation with real or complex coefficients has a set of real
or complex roots).
Gauss's method of mathematical proof that he used in these two magnificent
achievements marked the advent of the modern rigorous approach to
mathematics. Gauss's proofs were terse, thorough, and rigorous, and his
approach set the standard followed by later mathematicians.
About 1805 Gauss was asked to solve an important astronomical problem --
determining the orbit of an asteroid named Ceres. Ceres was difficult
to see with telescopes in use at that time and only fragmentary observations
of its orbit existed. Georg Wilhelm Hegel wrote a remarkable tract about
this time criticizing astronomers for not consulting philosophers. Hegel
believed that philosophy could "prove" that no further planets could
exist so there was no need to look for Ceres! (Hegel's later work was
used by Marx!) Gauss solved the problem using his method of least squares
(note that he fitted an elipse to the fragmentary data) and his unparalleled
ability at numerical computation. He forecast exactly where Ceres would
appear when it came from behind the sun and indeed he was exactly right.
This achievement caused a sensation in Europe comparable to the confirmation
of Einstein's famous theory of how gravity should bend light.
Sometime in the 1820s Gauss developed all the main results in
Non-Euclidean Geometry. These were not
known until after his death. About the same time he developed
The Intrinsic Differential Geometry of General
Curved Surfaces. These results allow the determination
of geodesic curves. These ideas were so powerful that they enabled the
development of Riemannian geometry, tensor analysis, and the ideas of
Einstein.
In the early 1830s Gauss developed modern
Complex Numbers ( a + ib). This and his
other work on numbers lead directly to modern algebraic number theory.
The above is only a fraction of Gauss's achievements. He also did
fundamental work on the theory of magnetism, the theory of functions
of a complex variable, and the theory of elliptic functions, just to
list a few areas. Much of the "wallpaper" of our advanced civilization
can be traced back to this colossal genius. As one author puts it:
"He surpassed the levels of achievement possible for ordinary men of
genius in so many ways that one sometimes has the eerie feeling that he
belonged to a higher species."
For more information on Gauss and other mathematicians, see the University
of St. Andrews website:
St. Andrews Website

