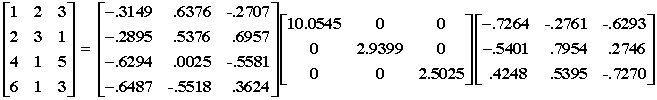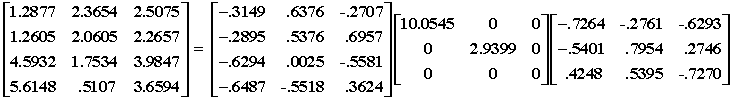The Eckart-Young Theorem
The Eckart-Young Theorem: Given an n by m matrix X of rank
r £ m £ n,
and its singular value decomposition,
ULV', where
U is an n by m matrix,
L is an m by m diagonal matrix of singular values,
and V is an m by m matrix such that
U'U = In and
V'V = VV' = Im
with the
singular values arranged in decreasing sequence
l1 ³
l2 ³
l3 ³ ...
³
lm ³ 0
then there exists an n by m matrix B of rank s,
s £ r, which minimizes the sum of the squared
error between the elements of X and the corresponding elements of
B when
B = ULsV'
where the diagonal elements of the m by m diagonal matrix
Ls are
l1 ³
l2 ³
l3 ³ ...
³
ls >
ls+1 =
ls+2 = ... =
lm = 0
Geometrically, the Eckart-Young Theorem states that the least squares
approximation in s dimensions of a matrix X can be found by replacing
the smallest m-s roots of
L with zeroes and remultiplying
ULV'.
For example, given:
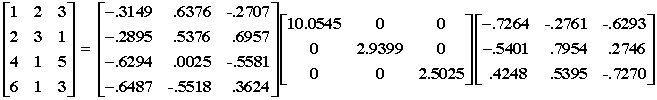
the rank 2 approximation is:
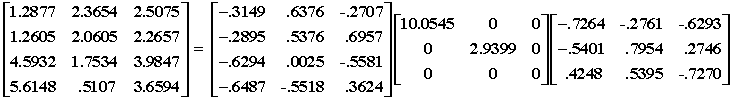
 svd_example.r -- R
Program to illustrate simple SVD.
svd_example.r -- R
Program to illustrate simple SVD.
svd_example.r looks like this:#
# file: svd_example.r
#
# Purpose: Simple R program showing Singular
# Value Decomposition
#
#
rm(list=ls(all=TRUE))
#
#
rc.file <- "c:/ucsd_course/svd_matrix.txt"
#
# Standard fields and their widths
#
rc.fields <- c("y1","y2","y3")
#
rc.fieldWidths <- c(3,3,3)
#
# Read the vote data from fwf
#
T <- read.fwf(file=rc.file,widths=rc.fieldWidths,as.is=TRUE,col.names=rc.fields)
dim(T)
#
nrow <- length(T[,1])
ncol <- length(T[1,])
#
xsvd <- svd(T)
#
# The Two Lines Below Put the Singular Values in a
# Diagonal Matrix -- The first one creates an
# identity matrix and the second command puts
# the singular values on the diagonal
#
Lambda <- diag(ncol)
diag(Lambda) <- xsvd$d
#
# Compute U*LAMBDA*V' for check below
#
XX <- xsvd$u %*% Lambda %*% t(xsvd$v)
#
xerror <- sum(abs(T-XX))
#